Тригонометрия пугает тождествами и функциями, которые на первый взгляд кажутся запутанными. На самом деле — это один из самых логичных и увлекательных разделов математики. Здесь важнее понимать логику, а не пытаться запоминать все формулы наизусть. Если научиться видеть связи и выводить одни соотношения из других, задачи будут решаться автоматически.
Разберем основные методы решения задач по тригонометрии на типовых примерах — сделаем акцент на объяснение. После прочтения сегодняшнего материала вы поймете внутреннюю логику предмета и научитесь самостоятельно проводить тригонометрические вычисления.
Основы тригонометрии: функции и их свойства
Начать изучение тригонометрии нужно с определения тригонометрических функций. Это конкретные зависимости, которые описывают реальные процессы вокруг нас: от колебаний маятника до движения планет.Представьте точку, которая равномерно движется по окружности. Ее координаты постоянно меняются, но по определенному закону.
Определение основных тригонометрических функций
В тригонометрии краеугольным камнем выступают три функции: синус, косинус и тангенс. Чтобы понять их смысл, удобно пользоваться единичной окружностью — радиусом 1 с центром в начале координат. Каждому углу на плоскости соответствует точка на этой окружности, и именно ее положение помогает определить функции:
- Косинус угла — это горизонтальная координата точки, то есть смещение вправо или влево от вертикальной оси.
- Синус угла — вертикальная координата, показывающая, насколько точка поднята вверх или опущена вниз относительно горизонтальной оси.
- Тангенс угла — отношение синуса к косинусу. Его можно наглядно представить как наклон прямой, соединяющей центр окружности с соответствующей точкой.
Свойства тригонометрических функций
Одно из главных свойств тригонометрических функций — периодичность. Она вытекает из движения по окружности. Пройдя круг полностью, мы возвращаемся в ту же точку, а значит, и значения функций повторяются:
- Синус и косинус повторяются каждые 2π радиан (360°).
- Тангенс составляет меньший период — π радиан (180°).
Еще одна важная характеристика — симметрия функций:
- Синус (нечетная): sin(-x) = -sin(x).
- Косинус (четная): cos(-x) = cos(x).
- Тангенс (нечетная): tg(-x) = -tg(x).
Знание четности и нечетности упрощает выражения, позволяя быстро найти значения функций для отрицательных углов.
Синус и косинус принимают значения от -1 до 1, тангенс может быть любым действительным числом.
Cинус и косинус определены для всех углов, а тангенс — для всех, кроме π/2 + πk.
Графики функций помогают закрепить все эти свойства наглядно:
- Синуса — волнообразная кривая, симметричная относительно начала координат;
- Косинуса — та же волна, но сдвинутая влево на четверть периода (π/2);
- Тангенса — периодически повторяющиеся ветви гиперболы с вертикальными асимптотами.
Основные формулы по тригонометрии
Существует четыре основные группы формул: основные идентичности, формулы приведения, формулы сложения и их производные. Каждая группа решает определенные типы задач и имеет свою область применения.
Главные тригонометрические идентичности
Решение задач по тригонометрии начинается с понимания главного равенства. Его называют основным тождеством:
sin²x + cos²x = 1
Оно следует из теоремы Пифагора для единичной окружности: сумма квадратов координат точки на окружности радиуса 1 равна 1. Именно поэтому формула работает для каждого угла — хоть маленького, хоть большого.
Запомните: тангенс — отношение синуса к косинусу, а котангенс — наоборот.:
- Tanx = sinx / cosx
- Cotx = cosx / sinx
Эти связи удобны, когда в задаче дана одна функция, а найти нужно другую. Например, если известен только синус, через формулу легко выразить косинус, а затем вычислить тангенс.
Важно помнить и про знаки функций. Они зависят от того, в какой четверти окружности находится угол:
- I четверть — все положительны.
- II четверть — положителен только синус.
- III четверть — только тангенс и котангенс.
- IV четверть — только косинус.
Формулы приведения и преобразования
Когда речь идет об углах больше 90°, на помощь приходят формулы приведения. Они позволяют выразить значения функций «больших» углов через острые углы.
Главный принцип: любой угол можно «свернуть» в первую четверть через симметрию окружности. При этом нужно учитывать два момента:
- В какой четверти лежит угол, таким будет и знак функции.
- Иногда функция заменяется на «соседнюю» — так называемую кофункцию (например, синус может превратиться в косинус).
Таблица: Формулы приведения для основных углов
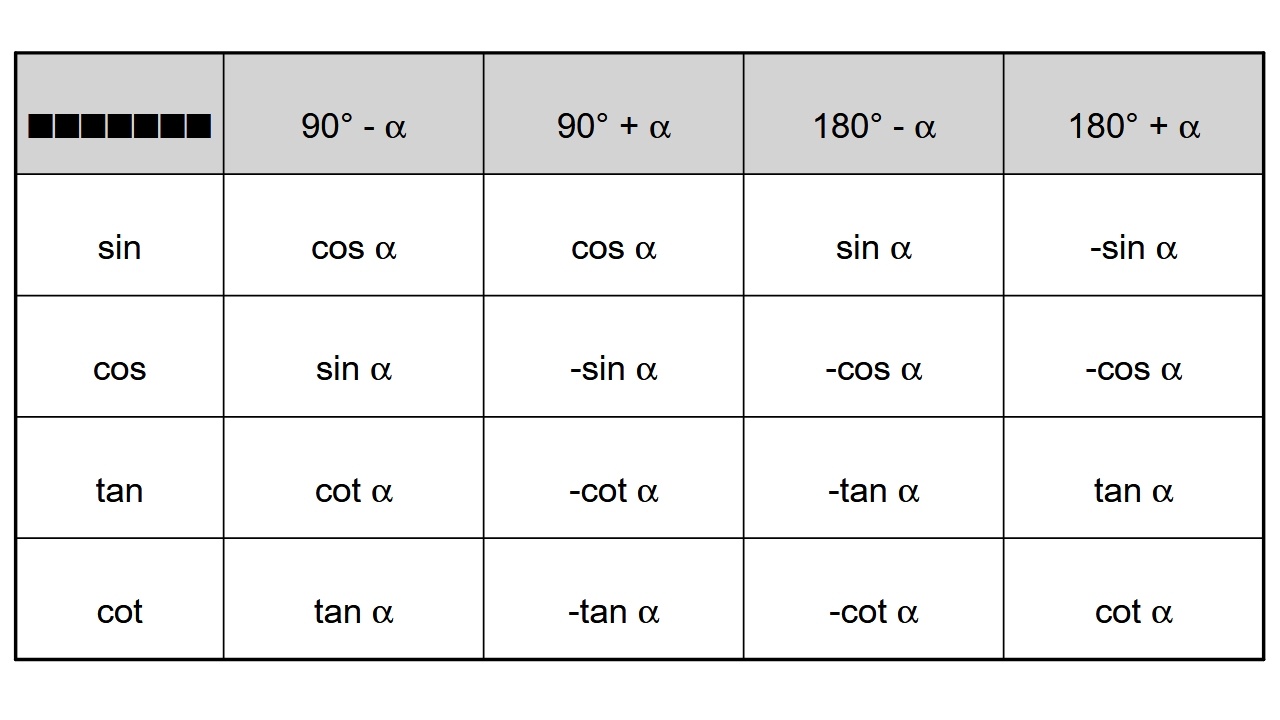
Методы решения задач по тригонометрии: системный подход
Задачи на упрощение выражений развивают алгебраические навыки и понимание связей между формулами. Здесь важно видеть возможности применения тождеств и преобразования. Часто помогает стратегия приведения к одному типу — например, выражение всего через синус и косинус.

Задачи на доказательство тождеств требуют творческого подхода и глубокого понимания формул. Стандартная стратегия — преобразование более сложной части равенства к виду более простой. Иногда полезно преобразовывать обе части к одному промежуточному виду.

Тригонометрические уравнения представляют наибольшую сложность. Они объединяют знание формул, понимание периодичности и умение работать с множественными корнями.

Универсальные методы решения
Алгоритм работы с любым тригонометрическим выражением начинается с внимательного анализа его структуры. Определите, какие функции входят в выражение, есть ли очевидные упрощения, можно ли применить основные тождества на первом этапе.
Для выражений с разными функциями часто помогает приведение к одному типу. Для выражений с кратными углами — использование формул двойного или половинного угла. Дробные выражения — приводим к общему знаменателю.
В результате ученик приводит уравнение к стандартному виду, находит корни в основном периоде, а затем записывает общее решение с учетом периодичности. Особое внимание требует выбор корней в заданном промежутке.
Решение задач по тригонометрии: практические примеры
Мы рассмотрим примеры разной сложности — от элементарных вычислений до многоэтапных преобразования. Каждый пример сопровождается пояснениями логики решения и альтернативными способами получения ответа.
Задачи на вычисление значений функций
Вычисление значений тригонометрических функций для нетабличных углов требует применения формул приведения. Ключевая идея — свести заданный угол к табличному, учитывая знак в соответствующей четверти.

Альтернативный способ решения таких задач — использование единичной окружности. Находим положение угла на окружности и определяем координаты соответствующей точки. Этот геометрический подход часто нагляднее алгебраического.
Для углов, не кратных 30° или 45°, используются формулы половинного угла или другие специальные приемы. Важно выбрать правильный знак результата, анализируя четверть, в которой лежит искомый угол.

Такие вычисления развивают понимание связей между формулами и учат выбирать оптимальный путь решения. Часто существует несколько способов получить ответ — выбор зависит от вашего уровня подготовки.
Тригонометрические уравнения: примеры решений
Существует несколько стандартных типов тригонометрических уравнений. Каждый тип имеет свои методы решения и формулы для записи ответа.
Простейшие тригонометрические уравнения
Начнем с вида sin x = a, cos x = a, tg x = a. Они являются базовыми. Для их решения существуют стандартные формулы, которые учитывают периодичность и дают все возможные корни.

Важно помнить об условиях существования решений. Для уравнений с синусом и косинусом необходимо |a| ≤ 1, для уравнений с тангенсом ограничений нет. При |a| > 1 первые два типа уравнений не имеют решений.
Запись ответа в тригонометрических уравнениях строгое. Нужно указать все семейства корней, используя целочисленный параметр. При решении в заданном промежутке следует выбрать конкретные значения параметра.
Работа с радианами и градусами требует внимательности. Убедитесь, что используете правильные единицы измерения углов. Переводы между ними — частый источник ошибок у начинающих.
Сложные тригонометрические уравнения
Уравнения, сводящиеся к квадратным, решаются заменой переменной. После решения вспомогательного алгебраического уравнения нужно вернуться к исходной переменной и решить получившиеся простейшие.
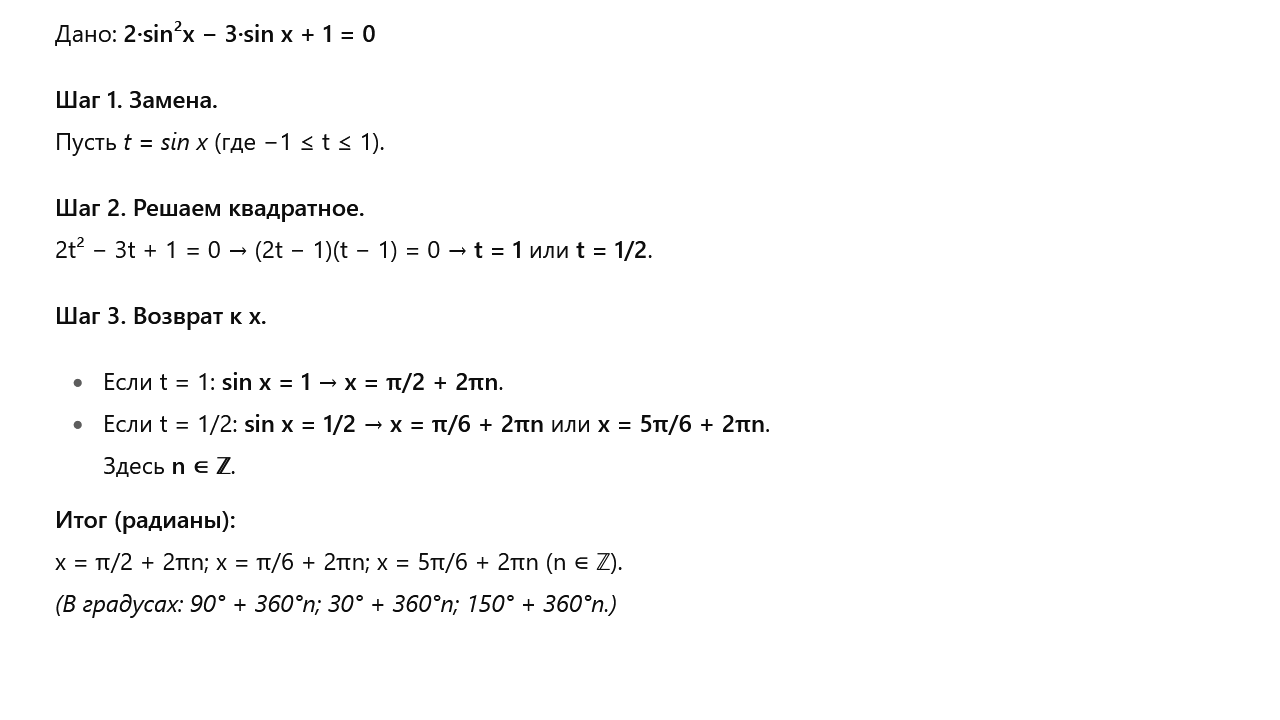
Уравнения, разложимые на множители, решаются через равенство произведения нулю. Каждый множитель приравнивается к нулю отдельно, что дает несколько простейших уравнений. Объединение их корней дает полное решение исходного уравнения.
Однородные уравнения решаются делением на степень одной из функций. Это приводит к уравнению относительно тангенса, которое часто оказывается квадратным. Важно не потерять корни, при которых знаменатель обращается в нуль.
Универсальная тригонометрическая подстановка превращает любое уравнение в рациональное относительно новой переменной. Этот метод всегда работает, но иногда приводит к громоздким вычислениям. Используйте его, когда другие способы не подходят.
Заключение
Тригонометрия раскрывает свою красоту тем, кто готов потратить время на понимание ее внутренней логики. За внешней сложностью формул скрывается стройная система взаимосвязанных понятий и теорем, основанная на простых геометрических идеях.
Успех в изучении тригонометрии зависит от нескольких ключевых факторов:
- Понимание связи с единичной окружностью на графиках — это дает геометрическую интуицию.
- Знание основных тождеств и формул преобразования — они составляют инструментарий для решения задач
- Регулярная практика на задачах разного уровня сложности.
Каждая решенная задача добавляет уверенности и расширяет арсенал методов. Начинайте с простого, постепенно усложняя материал. Не бойтесь делать ошибки — они неизбежны в процессе обучения и ведут к пониманию.
Вам нужна фриланс-биржа для работы, или вы хотите оформить студенческие работы на заказ? Студворк вам поможет, у нас есть специалисты любого уровня!





Комментарии