Многие считают алгебру одним из самых сложных предметов в школе. Испытывают панику перед контрольными работами и экзаменами, думая, что никогда не смогут разобраться в уравнениях и формулах.
Но что если мы скажем вам, что алгебра — это всего лишь набор простых правил и алгоритмов, которые может освоить каждый? Секрет успеха кроется не в особом таланте к математике, а в знании правильных методов решения.
Алгебра — это раздел математики, который изучает действия с числами, переменными и уравнениями. Многие учащиеся считают её сложной, но при правильном подходе любую алгебраическую задачу можно решить пошагово.
Базовые принципы решения алгебраических задач
Как решать задачи по алгебре? Успех в этом деле зависит от понимания основных правил. Главное правило — что делаешь с одной частью уравнения, то же самое делай с другой. Это сохраняет равенство.
Второй важный принцип — тот четкой порядок, по которому выполняются действия. Укажем его ниже.
- Действия в скобках.
- Возведение в степень.
- Умножение и деление.
- Сложение и вычитание.
Проверяйте полученный ответ, подставляя его в исходное уравнение.
Линейные уравнения
Это алгебраические выражения, где неизвестная величина присутствует только в первой степени. Общая формула записывается как ax + b = c, где a, b, c представляют собой известные числа, а x — искомое значение.
Основная стратегия решения заключается в изоляции переменной на одной стороне равенства. Для этого необходимо систематически переносить числовые значения в правую часть уравнения, а выражения с неизвестной — в левую.
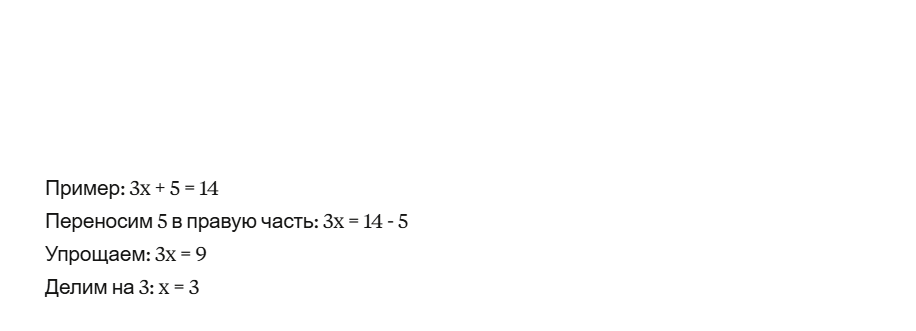
Квадратные уравнения
Содержат переменную во второй степени. Стандартный вид: ax² + bx + c = 0, где a ≠ 0.
Существует несколько способов по успешному решению квадратных уравнений. Самый универсальный — через дискриминант D = b² - 4ac.

Неполные квадратные уравнения
Заметили, что один из коэффициентов равен нулю? Вы столкнулись с уравнением, которое характеризуется как неполное. Они решаются проще.

Разложение на множители
Квадратное уравнение можно разложить на линейные множители? Это упрощает решение.

Теорема Виета
Для уравнения ax² + bx + c = 0 с корнями x₁ и x₂ справедливо:
x₁ + x₂ = -b/a
x₁ · x₂ = c/a
Эта теорема помогает проверить правильность найденных корней и иногда найти их без вычисления дискримина.
Системы уравнений
Это несколько уравнений с одними и теми же переменными. Решить систему значит найти значения переменных, которые удовлетворяют всем уравнениям одновременно.
Метод подстановки
Данный подход — один из наиболее понятных способов работы с системами алгебраических уравнений.
Суть методики состоит в том, что из любого уравнения системы выражается одна неизвестная через остальные переменные. Полученное выражение затем замещает соответствующую переменную в других уравнениях системы.

Метод сложения (алгебраического сложения)
Эта техника решения систем основана на принципе исключения одной переменной путём арифметических операций между уравнениями.
Метод эффективен в ситуациях, когда числовые коэффициенты при какой-либо переменной имеют одинаковые абсолютные значения или являются взаимно противоположными числами.

Графический метод
Геометрический подход к решению систем уравнений базируется на визуальном представлении каждого уравнения в виде линии на координатной плоскости. Искомое решение системы соответствует координатам точки, где происходит пересечение построенных линий.
Данный способ обладает высокой наглядностью, однако имеет ограничения в точности получаемых результатов.
Главное преимущество метода — быстрое определение количества решений:
- единственное решение возникает при пересечении линий;
- отсутствие решений — при параллельности линий;
- бесконечное множество решений — при совпадении линий.
Системы с тремя переменными
Для решения систем с тремя неизвестными используют те же методы, но применяют их последовательно для исключения переменных.
Пример:
x + y + z = 6
2x - y + z = 3
x + 2y - z = 1
Сначала исключаем z из первых двух уравнений, затем из первого и третьего. Получаем систему с двумя переменными и решаем её обычными методами.
Действия с многочленами
Многочлен представляет собой алгебраическое выражение, состоящее из суммы мономов (одночленов). Фундаментальные операции с полиномами включают сложение, вычитание, произведение и факторизацию.
При выполнении операций сложения и вычитания ключевым принципом является объединение мономов с идентичными степенными характеристиками. Операция умножения требует применения дистрибутивного закона для каждой пары слагаемых.
Разложение многочлена на простейшие множители служит мощным инструментом для упрощения выражений и решения полиномиальных уравнений.
Основные техники включают вынесение наибольшего общего делителя, применение стандартных формул сокращённого умножения и метод группировки слагаемых.
Рациональные уравнения
Характеризуются присутствием дробных выражений, в знаменателях которых содержатся переменные. Основная стратегия решения заключается в определении наименьшего общего кратного всех знаменателей и последующем умножении всех частей уравнения на это значение.
Критически важно предварительно установить область допустимых значений переменной. Поскольку деление на ноль невозможно, необходимо исключить все значения переменной, которые обращают любой знаменатель в нулевое значение.
После решения проверьте, не обращают ли найденные корни знаменатель в ноль.
Иррациональные уравнения
Здесь переменная под знаком корня. Основной метод решения — возвести в степень для избавления от корней.
Когда будете возводить в четную степень, могут появиться посторонние корни. Поэтому проверка важна в этом случае.

Показательные уравнения
Что мы видим здесь? Переменную — в показатели степени. Каков основной метод? Привести к одинаковому основанию.
Показательные уравнения содержат переменную в показателе степени. Основной метод — приведение к одинаковому основанию.

Логарифмические уравнения
Где переменная в этой категории уравнений? Под знаком логарифма. Используйте свойства логарифмов для упрощения.
Основное свойство: если log_a(x) = log_a(y), то x = y (при условии, что x > 0, y > 0).
Помните об области определения логарифма — аргумент должен быть положительным.
Практические советы
1. Ведите аккуратные записи. Пишите каждый шаг решения подробно. Это поможет избежать ошибок и легче найти их, если они возникнут.
2. Не торопитесь. Лучше потратить больше времени на понимание задачи, чем совершить ошибку из-за спешки.
3. Изучайте примеры задач по алгебре из учебников и решайте больше задач по алгебре с решениями. Практика — лучший способ освоить материал.
4. Создайте шпаргалку с основными формулами и алгоритмами. Держите её под рукой во время решения задач.
Алгоритмы решения основных типов задач
Для линейных уравнений следуйте простому алгоритму: перенесите все слагаемые с переменной влево, числа — вправо, приведите подобные, найдите переменную.
Как решать квадратные уравнения? Сначала проверьте, не является ли оно неполным. Если нет — вычислите дискриминант. При положительном дискриминанте используйте формулу корней.
Для систем уравнений определите, какой метод удобнее. Если коэффициенты при переменной равны или противоположны — используйте метод сложения. В остальных случаях — метод подстановки.
Как быть при работе с дробными уравнениями? Действовать в два этапа:
- Найти область допустимых значений.
- Умножить обе части на общий знаменатель.
Способы самопроверки
1. Самый надёжный способ проверки — подстановка найденного ответа в исходное уравнение. Если равенство выполняется, решение верное.
2. Используйте теорему Виета. Она пригодится при решении квадратных уравнений. Проверьте, равна ли сумма корней -b/a, а произведение c/a.
3. При решении систем подставьте найденные значения в каждое уравнение системы. Все равенства должны выполняться.
4. Оценивайте разумность ответа. Если по условию задачи переменная должна быть положительной, а получился отрицательный результат — ищите ошибку.
5. Проверяйте размерности в текстовых задачах. Если ищете скорость в км/ч, а получили отрицательное число — где-то ошибка.
Организация времени при решении задач
-
Прочитайте задачу целиком, прежде чем начать решение. Понимание общей картины экономит время.
-
Выделите 10-15% времени на планирование решения. Определите тип задачи и выберите метод решения до начала вычислений.
-
Решайте сначала простые задачи, затем переходите к сложным. Это поможет настроиться на работу и набрать уверенность.
-
Если задача не решается за 3-5 минут, отложите её и вернитесь позже. Свежий взгляд часто помогает найти решение.
-
Оставляйте 15-20% времени на проверку ответов. Лучше решить меньше задач, но без ошибок, чем много задач с неточностями.
-
При подготовке к контрольным засекайте время решения каждой задачи. Это поможет правильно распределить время на экзамене.
Подготовка к экзаменам
Для сдачи экзаменов, на которых и происходит решение уравнений по алгебре, повторите все основные темы. Уделите внимание типовым задачам по алгебре, которые часто встречаются в контрольных.
Решайте задачи на время. Это поможет научиться работать быстро и эффективно в условиях ограниченного времени.
Не зубрите формулы наизусть. Лучше понимайте, откуда они берутся и как применяются.
Типичные ошибки
Распространённая погрешность связана с некорректным переносом алгебраических выражений между частями уравнения. Зафиксируйте правило: при перемещении слагаемого его знак меняется на противоположный.
Ещё одна частая неточность возникает при раскрытии скобок с отрицательным коэффициентом. Когда перед скобками расположен знак минус, каждое слагаемое внутри скобок должно изменить знак на обратный.
При выполнении операций с дробными выражениями студенты часто допускают ошибки в процессе нахождения общего знаменателя или выполняют неправомерное сокращение дробей без учёта всех слагаемых.
Графическое решение уравнений
Графики функций помогают наглядно представить решение уравнений. Этот метод полезен для понимания количества корней и их приблизительных значений.
Для решения уравнения f(x) = g(x) нужно построить графики функций y = f(x) и y = g(x). Точки пересечения этих графиков дают корни уравнения.
Простейший пример — решение уравнения x² = 2x. Строим параболу y = x² и прямую y = 2x. Они пересекаются в точках (0; 0) и (2; 4), значит корни x₁ = 0 и x₂ = 2.
Графический метод помогает определить область существования корней перед точными вычислениями. Это экономит время и предотвращает ошибки.
Современные компьютерные программы позволяют строить сложные графики быстро и точно. Однако умение строить простые графики вручную остается важным навыком.
Использование калькуляторов и программ
Современные школьники имеют доступ к мощным вычислительным инструментам. Графические калькуляторы и математические программы упрощают решение сложных задач.
Важно понимать, что технические средства — это помощники, а не замена знаний. Сначала нужно освоить ручные методы решения, а потом использовать калькуляторы для проверки и ускорения вычислений.
Популярные программы для решения алгебраических задач включают GeoGebra, Wolfram Alpha, Desmos. Они позволяют строить графики функций, решать уравнения и проверять ответы.
При использовании калькуляторов проверяйте результат здравым смыслом. Технические ошибки ввода могут привести к неправильным ответам.
Научитесь пользоваться основными функциями научного калькулятора: работа со степенями, корнями, логарифмами и тригонометрическими функциями.
Заключение
Овладение навыками решения алгебраических задач представляет собой постепенный процесс, требующий систематической тренировки и накопления опыта. Фундамент успеха — понимание базовых принципов и освоение методик работы с уравнениями по алгебре.
Ошибки — неотъемлемая составляющая учебы. Воспринимать их нужно как возможности для углубления знаний и совершенствования навыков. Тогда алгебра станет доступнее и понятнее. Конечно же, при условии методичной работы и постоянной практики.
Вам нужна фриланс-биржа для работы или хотите оформить решение задач на заказ?





Комментарии