
Геометрия — одна из старейших областей математики, изучающая свойства фигур на плоскости и в пространстве. Она зарождалась еще в Древнем Египте и получила статус науки уже в Древней Греции (около 4000 лет назад). Понимание этого предмета строится не столько на заучивании теорем, сколько на умении видеть закономерности и применять логическое мышление. В этом материале мы рассмотрим основные положения науки и пошагово разберем примеры решений задач по геометрии.
Основные принципы решения геометрических задач

1. Внимательное чтение условия
Первый и самый важный шаг — тщательно прочитать условие задачи. Многие ошибки школьников возникают именно из-за невнимательности на этом этапе.
Что нужно делать:
- Прочитайте задачу несколько раз;
- Выделите ключевые слова и фразы;
- Определите, что дано и что нужно найти;
- Обратите внимание на единицы измерения.
2. Построение чертежа
Чертеж переносит условие на бумагу и наглядно показывает действия для выполнения задания.
Правила построения чертежа:
Используйте линейку и циркуль для точности;
- Обозначайте все данные элементы;
- Соблюдайте пропорции (если это возможно);
- Выделяйте искомые элементы цветом или штриховкой;
- Подписывайте все точки, стороны и углы.
3. Анализ данных
После построения чертежа проанализируйте имеющиеся данные:
- Какие элементы известны?
- Какие свойства фигур можно использовать?
- Какие теоремы применимы к данной ситуации?
4. Составление плана решения
Определите последовательность действий:
- Какие промежуточные результаты нужно получить?
- В каком порядке применять формулы?
- Нужны ли дополнительные построения?
Ключевые теоремы и их применение

Предположим, нужно определить длину лестницы, чтобы добраться до окна второго этажа. Расстояние от стены до основания лестницы равно 3 м, а высота до окна — 4 м. Задача сводится к прямоугольному треугольнику: основание — 3 м, высота — 4 м, а гипотенуза — это искомая длина лестницы. По теореме Пифагора:
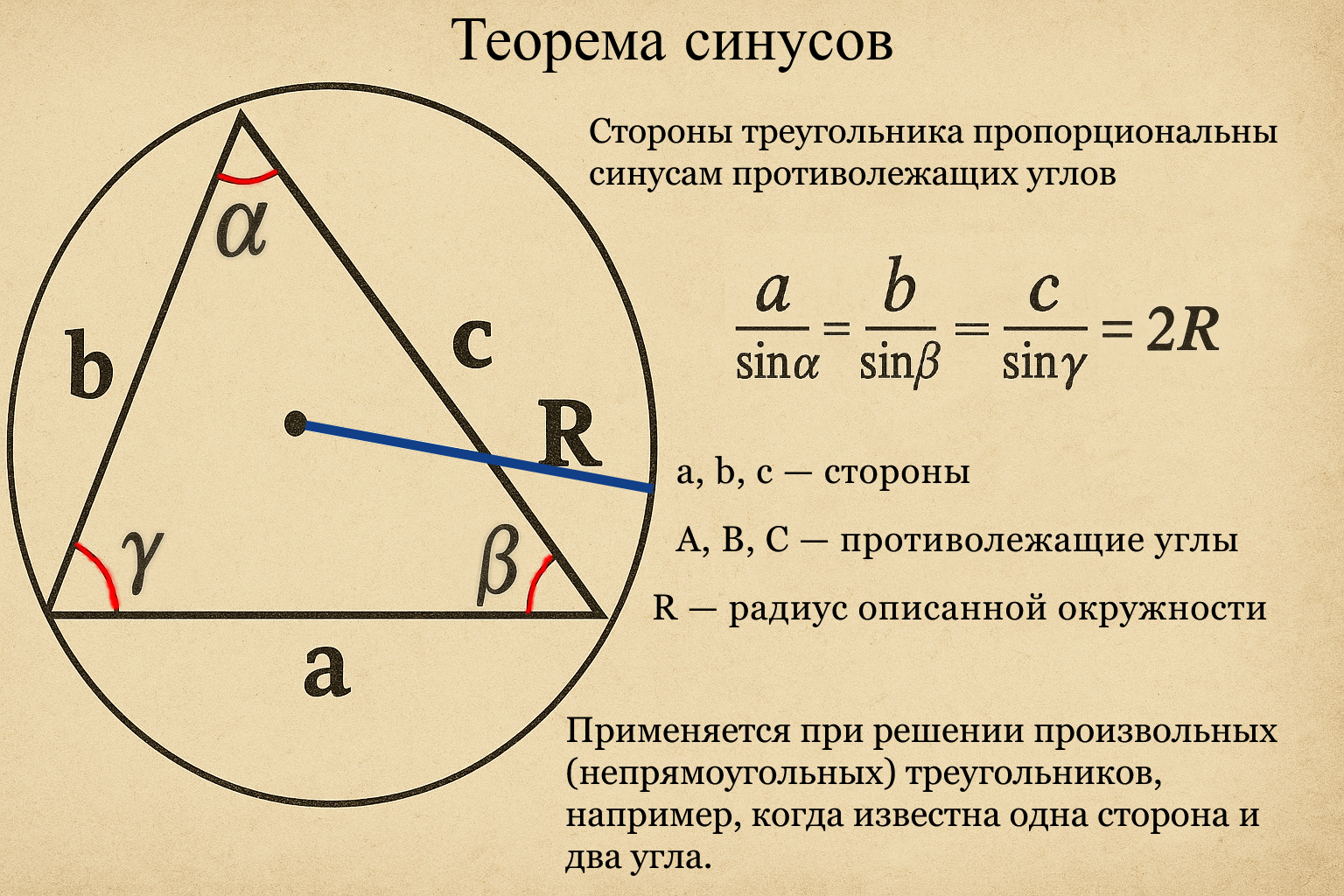
Например, в треугольнике ABC угол A = 40°, угол B = 75°, сторона a = 8 см. Нужно найти сторону b.
Сначала определим угол C:
C = 180° − (40° + 75°) = 65°.
Теперь применим теорему синусов:
Подставим значения:
b = 12 см
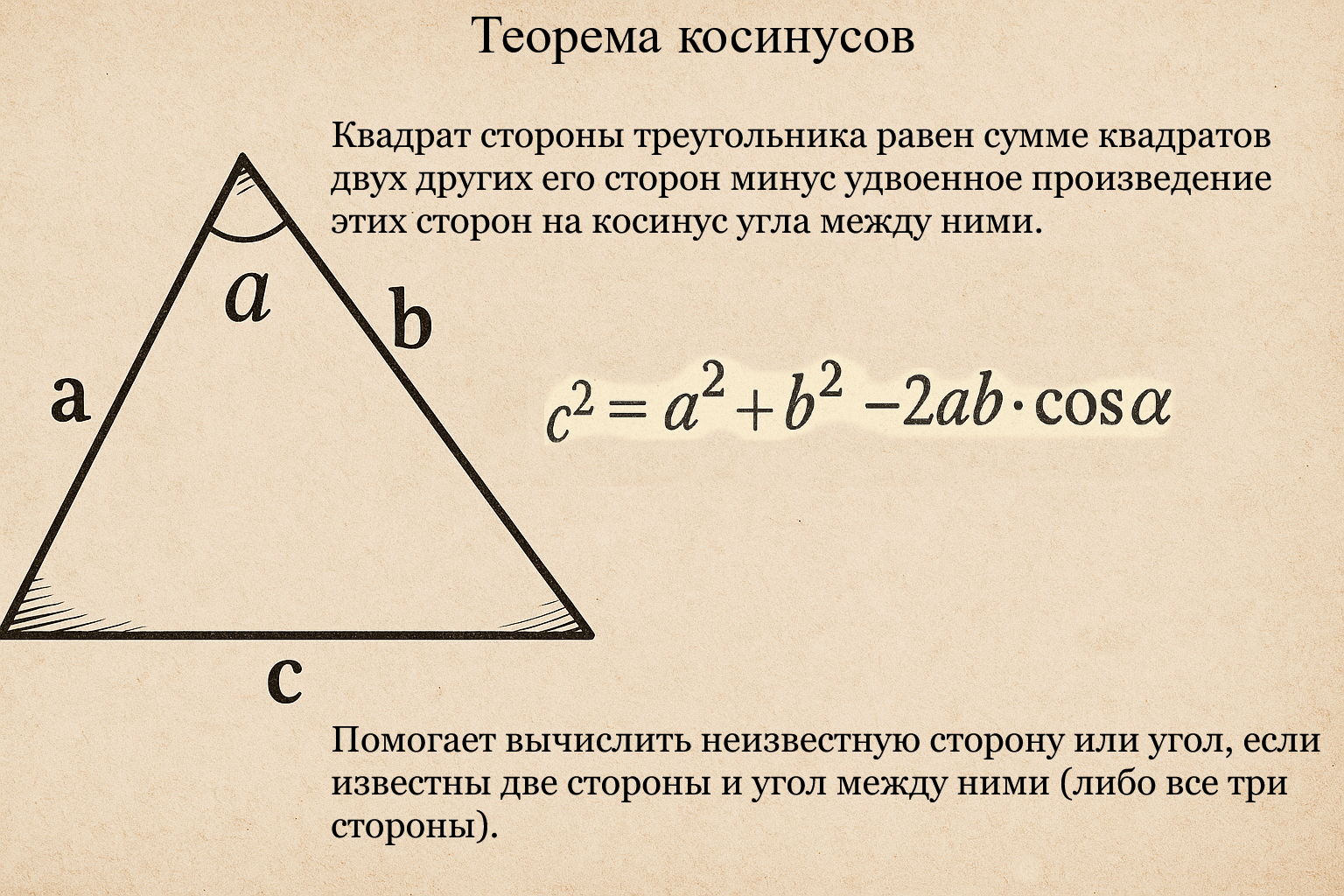
Например, в треугольнике XYZ известны стороны: XY = 7 см, YZ = 9 см, а угол между ними ∠Y = 120°. Нужно найти сторону XZ.
По теореме косинусов:
XZ² = XY² + YZ² − 2 · XY · YZ · cos ∠Y.
Подставим значения:
XZ² = 7² + 9² − 2 · 7 · 9 · cos 120°.
Так как cos 120° = −0,5, получаем:
- XZ² = 49 + 81 − 2 · 7 · 9 · (−0,5).
- XZ² = 130 + 63 = 193.
- XZ = √193 ≈ 13,9 см.
XZ ≈ 13,9 см
Основные типы геометрических задач
Задача на вычисление
Найти числовое значение некоторого элемента фигуры. Учитель часто включает такие задачи в контрольную работу для учеников старших классов.
Пример 1. Вычислить площадь треугольника
В треугольнике XYZ угол Y = 90°, катеты XY = 5 см, YZ = 12. Найдите площадь треугольника.
Решение:
- Рисунок. Строим прямоугольный треугольник с прямым углом в точке Y;
- Анализ. Известны два катета;
- Формула. S = (1/2) × a × b, где a и b — катеты;
- Вычисление. S = (1/2) × 5 × 12 = 30 см².
30 см²
Задача на доказательство
Логически обосновать некоторое утверждение. Такие примеры часто встречаются в программе старших классов.
Пример 2. Доказать равенства треугольников
В треугольниках MNP и KLM известно: MN = KL, NP = LM, MP = KM. Докажите, что треугольники равны.
Решение:
- Дано: MN = KL, NP = LM, MP = KM.
- Доказать: △MNP = △KLM
- Доказательство: по третьему признаку равенства треугольников (по трем сторонам) — если все стороны одного треугольника равны соответствующим сторонам другого треугольника, то такие треугольники равны.
MNP = △KLM по третьему признаку равенства треугольников.
Задача на построение
Построить фигуру с заданными свойствами. Создание точного рисунка — ключевой навык для таких задач.
Пример 3: Построение перпендикуляра
Построить биссектрису данного угла ∠ABC.
Решение:
- Вершину угла B принимаем за центр и проводим дугу окружности, которая пересечет стороны угла BA и BC в точках E и F.
- Из точек E и F проводим дуги одинакового радиуса так, чтобы они пересеклись в точке D.
- Соединяем точку B с точкой D.
- Прямая BD является биссектрисой угла ∠ABC.
Биссектриса делит угол ∠ABC на два равных угла.
Задачи по геометрии: примеры с решением
Рассмотрим, как решать задачи по геометрии на конкретных примерах с детальным анализом каждого действия.
Задача на площадь и стороны равнобедренного треугольника

В равнобедренном треугольнике XYZ (XY = YZ) основание XZ = 14 см, а высота YH = 9 см. Найдите площадь треугольника и длины боковых сторон.
Рисуем равнобедренный треугольник XYZ:
- XY = YZ (боковые стороны);
- XZ = 14 см (основание);
- YH ⊥ XZ, YH = 9 см.
Вычисляем площадь:
- S = (1/2) × основание × высота;
- S = (1/2) × 14 × 9 = 63 см².
Находим боковые стороны:
В равнобедренном треугольнике высота делит основание пополам: XH = HZ = XZ/2 = 7 см
Рассмотрим прямоугольный треугольник XYH по теореме Пифагора:
- XY² = XH² + YH²
- XY² = 7² + 9² = 49 + 81 = 130
- XY = √130 ≈ 11,4 см
Так как XY = YZ, то обе боковые стороны приблизительно равны 11,4 см.
S = 63 см², XY = YZ ≈ 11,4 см
Задача на окружность (пересекающиеся хорды)

В окружности с центром O проведены две хорды MN и KL, которые пересекаются в точке Q. Известно, что MQ = 5 см, QN = 7 см, KQ = 10 см. Найдите длину отрезка QL.
Теоретическая база:
По теореме о пересекающихся хордах: произведение длин отрезков одной хорды равно произведению длин отрезков другой хорды.
Применение теоремы:
- MQ × QN = KQ × QL
- 5 × 7 = 10 × QL
- 35 = 10 × QL
- QL = 3,5 см
QL = 3,5 см
Задача с параллелограммом

В параллелограмме ABCD диагонали AC и BD пересекаются в точке O. Известно, что AB = 10 см, AD = 6 см, угол BAD = 60°. Найдите длины диагоналей параллелограмма.
Анализ данных:
- ABCD — параллелограмм
- AB = 10 см, AD = 6 см
- ∠BAD = 60°
- Нужно найти AC и BD
Находим диагональ AC через треугольник ABC:
- BC = AD = 6 см (противоположные стороны параллелограмма равны)
- ∠ABC = 180° - 60° = 120° (смежные углы параллелограмма)
AC² = AB² + BC² - 2·AB·BC·cos(∠ABC)
AC² = 10² + 6² - 2·10·6·cos(120°)
AC² = 100 + 36 - 120·(-0.5) = 136 + 60 = 196
AC = 14 см
Находим диагональ BD через треугольник ABD
BD² = AB² + AD² - 2·AB·AD·cos(∠BAD)
BD² = 10² + 6² - 2·10·6·cos(60°)
BD² = 100 + 36 - 120·0.5 = 136 - 60 = 76
BD = 2√19 ≈ 8.72 см
AC = 14 см, BD = 2√19 см
Типичные ошибки и как их избежать
При решении задач по геометрии школьники сталкиваются с одними и теми же затруднениями. Ошибки возникают как из-за невнимательности, так и из-за недостаточного понимания теории. Чтобы повысить точность решений и сократить количество неверных ответов, рассмотрим типичные ошибки и разберем практические способы, которые помогут избежать их в дальнейшем.
- Неточный чертеж.
Многие решают задачу «в уме» или строят схему наспех. В итоге легко перепутать элементы. Всегда выполняйте аккуратный чертеж с обозначениями, даже если условие кажется простым. - Неверное применение теорем.
Школьники часто путают условия применения теорем Пифагора, синусов и косинусов. Перед использованием формулы убедитесь, что треугольник подходит под условия теоремы.
- Ошибки при вычислениях.
Потерянный знак, неправильно рассчитанный квадрат или корень — частая причина неверного ответа. Проверяйте ключевые шаги, выполняйте промежуточные расчеты письменно. - Игнорирование свойств фигур.
Многие забывают, что в равнобедренном треугольнике высота к основанию делит его пополам. Перед решением вспомните основные свойства фигур, упрощайте задачу через них. - Поспешные выводы без доказательств.
Иногда ученики записывают ответ, не обосновав шаги. Всегда приводите рассуждения и указывайте, на каких признаках или формулах основано решение. - Неправильное использование масштаба в построениях.
Ошибка возникает, когда чертеж «на глаз» искажает пропорции. Не доверяйте картинке целиком, используйте только формулы и доказательства.
Советы для успешного решения задач
Чтобы справляться с заданиями увереннее, полезно придерживаться единого алгоритма решения. Так вы сократите количество ошибок, улучшите логику рассуждений и добьетесь точного результата. Разберем практические советы, которые помогут выработать системный стиль работы с геометрическими задачами:
- Начинайте с чертежа
Даже простая схема помогает наглядно увидеть взаимосвязь элементов, избежать путаницы. - Переписывайте условие задачи своими словами
Это улучшает понимание, помогает заметить ключевые данные, которые могут быть упущены при беглом чтении. - Используйте свойства фигур
Вспоминайте признаки равенства и подобия треугольников, свойства параллелограмма, трапеции, окружности — на них строится задание. - Применяйте теоремы по назначению
Прежде чем подставлять данные в формулу, убедитесь, что условия задачи соответствуют применяемой теореме. - Записывайте рассуждения пошагово
Лаконичные, но четкие объяснения поддерживают логику, позволяя легко выявить ошибку в ходе проверке. - Проверяйте результат
Сравните ответ с исходными данными: если число выглядит слишком большим или маленьким, стоит перепроверить вычисления. - Регулярно тренируйтесь
Чем больше задач разного уровня сложности вы решите, тем быстрее выработаете «геометрическое чутье».
Заключение
Геометрия — это наука о математических закономерностях, формирующая способность к абстрактному мышлению. Полученные навыки (следование логике, систематический подход) пригодятся не только в изучении математики, но и в повседневной жизни.
Успех в решении задач по геометрии приходит с практикой. Главное — не торопиться, внимательно анализировать условие, строить рисунок и последовательно применять изученные теоремы. Продолжайте решать задачи, экспериментировать с различными подходами и не бойтесь делать ошибки — они являются важной частью процесса обучения. Удачи в изучении геометрии!
Вам нужна флиранс-биржа для работы, или вы хотите заказать решение задач?





Комментарии