После этой статьи вы увидите: даже самые замысловатые уравнения можно разложить на понятные шаги. В статье расскажем, как решать сложные дроби, используя понятный порядок действий и проверенные приёмы.Материал подойдёт школьникам и студентам, которым важно понять логику действий и научиться уверенно работать с примерами. Конкретные методы, разбор ошибок и приёмы, которые ускорят счёт.
Что такое сложные дроби
Сложная дробь — это выражение, в котором в числителе или знаменателе находится другое дробное число. Такой тип записи часто встречается в уравнениях и задачах, и его можно преобразовать в более простой вид для удобства вычислений.
Пример:
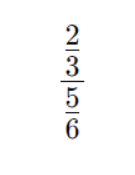
Во многих примерах встречаются выражения с переменными и дробными частями в числителе или знаменателе. Такие конструкции требуют предварительного упрощения, чтобы переход к решению был быстрым и точным.
Свойства
Перед тем как браться за примеры, стоит вспомнить несколько правил:
- Сокращение: числитель и знаменатель можно уменьшить, разделив на один и тот же делитель.
- Умножение: выражения перемножаются «крест-накрест» – числитель с числителем, знаменатель с знаменателем.
- Деление: нижний пример переворачивается, и операция превращается в умножение.
- Приведение к общему знаменателю: нужно для сложения и вычитания.
Принцип работы со сложными дробями: пошаговый подход
- Работа со сложными примерами строится по алгоритму:
- Преобразовать все смешанные числа в неправильные выражения.
- Упростить каждую часть — числитель и знаменатель.
- Если нужно делить, заменить деление на умножение на обратную.
- Сократить общие множители.
Такой порядок помогает и при решении задач, и когда нужно понять как решать сложные примеры с дробями. Главное – не спешить и на каждом этапе проверять, можно ли упростить выражение ещё.
Как упрощать и перестраивать
Преобразование – это набор приёмов, которые помогают сделать пример проще и понятнее. Без этих шагов любая задача превращается в громоздкое вычисление. Разберём основные ситуации. Если освоить их, легко понять, как научиться решать сложные дроби.
Для сложения и вычитания
- Привести к общему знаменателю.
- После сложения или вычитания упростить результат, если есть общий множитель.
чем раньше найдёте общий знаменатель, тем меньше будет вычислений.
Для умножения
- Перемножить числители между собой.
- Перемножить знаменатели между собой.
- Сократить результат, если возможно.
Полезно сокращать до умножения – это экономит время и снижает риск ошибки.
При делении
Деление заменить умножением на обратную дробь.
Применить правила умножения.
- Такое преобразование делает любую задачу проще и помогает быстрее двигаться к ответу.
При сокращении
- Найти общий множитель в числителе и знаменателе.
- Разделить обе части на него.
Чем раньше сокращаете, тем меньше придётся считать в следующих шагах.
Приёмы упрощения
Чтобы быстрее понять, как решать сложные дроби, важно научиться их упрощать до максимально простого вида. Это экономит время и снижает риск ошибок.
- Ищите общий множитель сразу. Перед любыми действиями проверьте, есть ли число или выражение, на которое можно сократить числитель и знаменатель. Иногда это убирает целый этап вычислений.
- Разделяйте громоздкие примеры. Если числитель или знаменатель состоит из суммы или разности, попробуйте разложить их на отдельные части. Так проще следить за каждым элементом и упрощать их по отдельности.
- Заменяйте смешанные числа. Любое смешанное число лучше перевести в неправильную дробь. Это делает формулы компактнее и удобнее для работы.
- Работайте от простого к сложному. Начинайте с самых маленьких преобразований — сокращений, упрощения отдельных частей. Только потом переходите к более длинным вычислениям.
Как решать сложные дроби: пошагово
Разберём порядок действий, который помогает без спешки и ошибок дойти до ответа. Он подойдёт для любых задач, где есть дробные выражения, и поможет понять, как решать сложные дроби на практике.
Преобразование составных выражений
Если в числителе или знаменателе стоит ещё одна дробь, сначала превращаем всё в простую форму. Для этого деление заменяем умножением на обратную, а смешанные числа переводим в неправильные.
Работа с числителем и знаменателем
Числитель и знаменатель упрощаем отдельно. Это значит — выполняем действия внутри каждой части, пока они не станут проще. Если в них есть скобки, сначала раскрываем их.
Приведение к общему знаменателю
Когда в уравнении встречается несколько дробных выражений, их приводят к общему знаменателю. Для этого находят наименьшее общее кратное знаменателей и умножают каждую часть на нужный множитель. Такой шаг позволяет объединить элементы и упростить последующие вычисления.
Упрощение выражений
После всех преобразований проверяем, можно ли сократить общий множитель. Чем меньше числитель и знаменатель, тем быстрее получится итоговый ответ.
Лайфхаки по решению задач с дробями
Эти советы помогут быстрее разобраться со сложными выражениями и избежать лишних ошибок:
- Сокращайте на каждом шаге. Чем меньше числа, тем проще считать и меньше риск запутаться.
- Проверяйте знаки. Минусы часто становятся причиной неверного ответа, особенно при работе со скобками.
- Записывайте промежуточные шаги. Даже если выражение выглядит несложным, полезно записывать каждый шаг решения. Это помогает заметить неточность на раннем этапе и избежать ошибок в конечном ответе.
- Начинайте с простого. Если выражение громоздкое, упростите хотя бы одну часть, чтобы расчёты стали легче.
- Используйте обратные дроби сразу. Не откладывайте их преобразование — так экономите время и избегаете лишних действий.
- Разбивайте задачу на этапы. Решайте уравнение блоками: сначала преобразование, потом упрощение, затем подсчёт.
Примеры решения задач
Подборка примеров поможет закрепить теорию и показать, как решать сложные уравнения с дробями шаг за шагом. Такой разбор делает применение правил в вычислениях понятным и наглядным.
Задача 1
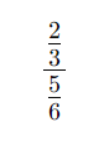
Деление заменяем умножением на обратную:
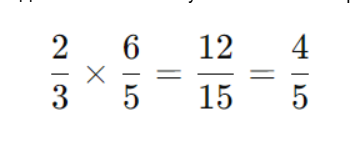
Задача 2
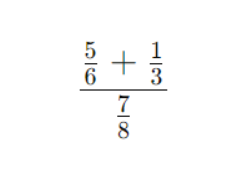
Сначала считаем числитель:
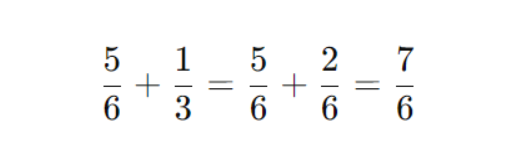
Делим на ⅞:
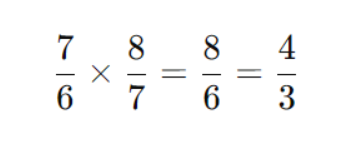
Задача 3
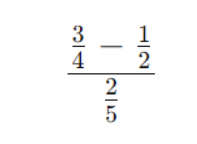
В числителе:
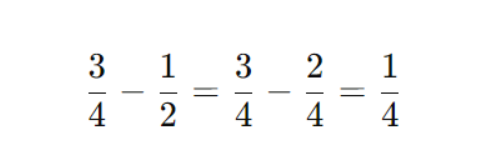
Делим на ⅖:
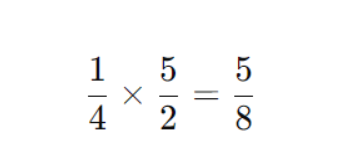
Задача 4
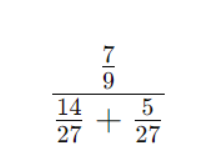
В знаменателе:
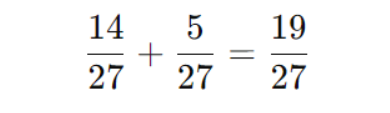
Делим:
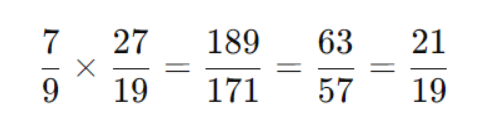
Задача 5
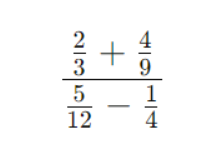
Числитель:
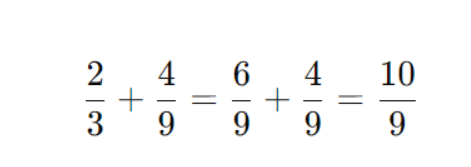
Знаменатель:
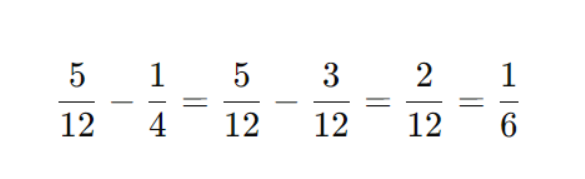
Делим:
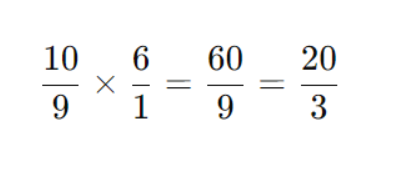
Итоги
Мы разобрали в статье, как решать сложные дроби: сначала преобразовать составные части, затем привести выражения к общему знаменателю, упростить и только после этого выполнить вычисления. Такой алгоритм делает задачу последовательной и управляемой. Рассмотренные свойства, приёмы и примеры помогают уверенно справляться даже с громоздкими выражениями. А если понадобится проверить решение или оформить его без ошибок, эксперты Студворка помогут решить задачу быстро и качественно.



Комментарии