Как найти площадь ромба: расчёты с формулами и онлайн-калькулятор

Перед тем как перейти к формулам и расчётам, нужно разобраться, что такое площадь ромба и почему этот показатель так важен в геометрии. В учебных задачах часто встречается вопрос: какая площадь ромба и как её найти. Под площадью понимают числовое значение, которое показывает, сколько места фигура занимает на плоскости.

Существует несколько способов, как найти площадь ромба — через стороны, высоты, диагонали и углы. Каждый метод имеет свои особенности и применяется в зависимости от условия задачи.

Ромб — это параллелограмм, в котором все стороны равны друг другу.

Что такое площадь ромба

Площадь ромба — это числовое значение, которое показывает, сколько места занимает фигура на плоскости. В геометрии её часто требуется находить в задачах, и здесь важно знать разные способы расчёта.

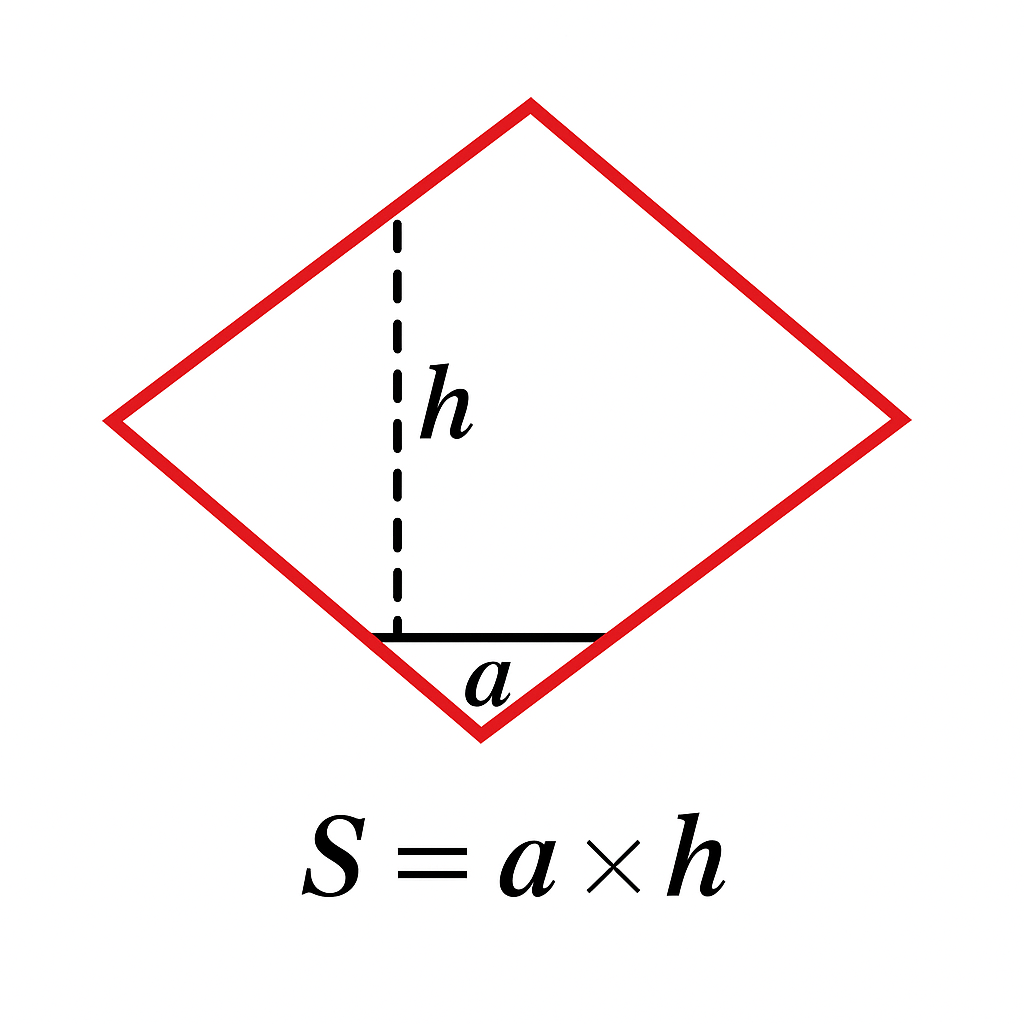
Основная формула площади ромба:

$S = a \times h$

где $a$ — длина стороны ромба, $h$ — проведённая к ней высота.

Также часто используется универсальная формула через диагонали:

$S = \frac{d_1 \times d_2}{2}$

где $d_1$ и $d_2$ — диагонали ромба.

Таким образом, зная либо сторону и высоту, либо диагонали, можно легко вычислить площадь фигуры.

Онлайн-калькулятор площади ромба

Если стороны ромба образуют прямой угол, то получим квадрат.

Диагонали ромба пересекаются под прямым углом.
Диагонали ромба являются биссектрисами его углов.

Площадь ромба, как и площади большинства геометрических фигур, можно найти несколькими способами. Разберемся в их сути и рассмотрим примеры решений.

Формула площади ромба по стороне и высоте

Пусть нам дан ромб со стороной $a$ и высотой $h$, проведенной к этой стороне. Так как ромб это параллелограмм, то его площадь мы находим так же, как и площадь параллелограмма.

Решим простой пример.

Пример

Сторона ромба равна 5 (см.). Высота, опущенная к этой стороне, имеет длину 2 (см.). Найти площадь ромба $S$.

Решение

$a=5$
$h=2$

Пользуемся нашей формулой и вычисляем:
$S=a\cdot h=5\cdot 2=10$ (см. кв.)

Ответ: 10 см. кв.

Формула площади ромба через диагонали

Здесь все так же просто. Нужно просто взять половину произведения диагоналей и получить площадь.

Пример

Одна из диагоналей ромба равна 7 (см.), а другая в 2 раза больше первой. Найдите площадь фигуры.

Решение

$d_1=7$
$d_2=2\cdot d_1$

Найдем вторую диагональ:
$d_2=2\cdot d_1=2\cdot 7=14$
Тогда площадь:
$S=\frac{1}{2}\cdot7\cdot14=49$ (см. кв.)

Ответ: 49 см. кв.

Формула площади ромба через две стороны и угол между ними

Пример

Найти площадь ромба, если каждая из его сторон равна 10 см, а угол между двумя смежными сторонами равен 30 градусам.

Решение

$a=10$
$\alpha=30^{\circ}$

По формуле получаем:
$S=a^2\cdot\sin(\alpha)=100\cdot\sin(30^{\circ})=50$ (см. кв.)

Ответ: 50 см. кв.

Формула площади ромба по радиусу вписанной окружности и углу

Пример

Найти площадь ромба, если угол между основаниями равен 60 градусов, а радиус вписанной окружности - 4 (см.).

Решение

$r=4$
$\alpha=60^{\circ}$

$S=\frac{4\cdot r^2}{\sin(\alpha)}=\frac{4\cdot 16}{\sin(60^{\circ})}\approx73.9$ (см. кв.)

Ответ: 73.9 см. кв.

Формула площади ромба по радиусу вписанной окружности и стороне

Пример

Возьмем условие из предыдущей задачи, но пусть вместо угла нам известна сторона ромба, равная 5 см.

Решение

$a=5$
$r=4$

$S=2\cdot a\cdot r=2\cdot5\cdot4=40$ (см. кв.)

Ответ: 40 см. кв.

Срочно нужна помощь с математикой? Наши эксперты выполнят задания за 2 часа.

Тест на тему “Площадь ромба”