Сложение комплексных чисел

Алгебраическая формула

Любые два вещественных числа можно сложить, и результатом сложения тоже является вещественное число. Это же верно и для комплексных чисел: любые два комплексных числа можно сложить, и их сумма (результат сложения) — это комплексное число. Причем сложение комплексных чисел сводится к сложению вещественных чисел. А именно: пусть даны два комплексных числа

$z_1 =x_1 +iy_1, z_2 =x_2 +iy_2.$

Их сумма — это комплексное число, определяемое формулой

$z_1+z_2 = (x_1+x_2) +i(y_1+y_2).$

Таким образом, вещественная часть суммы комплексных чисел — это сумма вещественных частей слагаемых, и мнимая часть суммы комплексных чисел — сумма мнимых частей слагаемых. Это тоже можно записать в виде формул:

$\mathrm{Re}\left(z_1+z_2\right) = \mathrm{Re}\,z_1 + \mathrm{Re}\,z_2, \quad$

$\mathrm{Im}\left(z_1+z_2\right) = \mathrm{Im}\,z_1 + \mathrm{Im}\,z_2.$

Для комплексных чисел, как и для вещественных, определена операция вычитания. Найти разность $z_1-z_2$ — это все равно что найти сумму $z_1+(-z_2)$, где число $-z_2$ получается из $z_2$ сменой знака вещественной и мнимой частей.

Геометрическая интерпретация сложения

Нам известно, что каждому комплексному числу $x+yi$ соответствует точка плоскости с координатами $(x,y)$. Вектор, проведенный от начала координат к точке $(x,y)$, называется радиус-вектором этой точки. Радиус-вектор точки $(3,2)$, соответствующей комплексному числу $3+2i$, изображен на следующем рисунке:

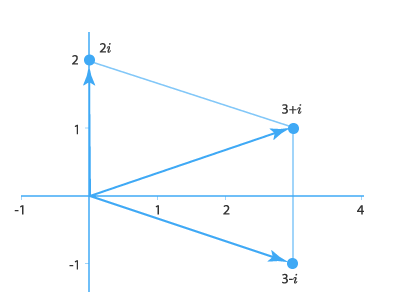
При сложении комплексных чисел соответствующие им радиус-векторы тоже складываются. Изобразить это на рисунке можно с помощью известного правила параллелограмма. На следующем рисунке с помощью векторов проиллюстрировано сложение комплексных чисел $(3-i) + 2i = 3+i$:

Решение примеров на сложение комплексных чисел

Пример 1

Найти сумму комплексных чисел $z_1+z_2$, где:

$a) \ z_1 = 3+2i, z_2 = 5-i;$

$b) \ z_1 = -i, z_2 = 4+i;$

$c) \ z_1 = -3-4i, z_2 = 3+5i.$

Решение
$a) \ z_1 + z_2 = (3+2i) + (5-i) = (3+5) + (2-1)i = 8+i;$

$b) \ z_1 + z_2 = (-i) + (4+i) = (0+4) + (-1+1)i = 4 + 0 \cdot i = 4;$

$c) \ z_1 + z_2 = (-3-4i) + (3+5i) = (-3+3) + (-4+5)i = 0+i =i.$

Пример 2

Найти разность комплексных чисел $z_1-z_2$, где:

$a) \ z_1 = 3+2i, z_2 = 5-i;$

$b) \ z_1 = -i, z_2 = -3-2i.$

Решение

$a) \ z_1 - z_2 = (3+2i) - (5-i) = (3-5) + (2-(-1))i = -2+3i;$

$b) \ z_1 - z_2 = (-i) + (-3-2i) = (0-(-3)) + (-1-(-2))i = 3 + i.$

Заказать статью по математике у экспертов биржи Студворк!